Persamaan garis lurus merupakan salah satu bagian dalam pembelajaran matematika di SMP. Sebagai salah satu mata pelajaran baru di SMP, persamaan garis lurus dianggap sebagai mata pelajaran yang sifatnya bastrak dan memiliki tingkat kesulitan tinggi. Salah satu cara untuk mengatasi hal tersebut adalah banyak berlatih menyelesaikan soal-soal yang berhubungan dengan gradien dan persamaan garis lurus Oleh sebab itu, pada kesempatan kali ini penulis ingin berbagi soal latihan mengenai gradien dan persamaan garis lurus. Selain itu, penulis menambahkan beberapa nomor mengenai soal sistem persamaan linier dua variabel (SPLDV) sebagai bonus. Semoga bermanfaat!
Atau dapat juga mengunduhnya disini
Mari kita jadikan matematika sebagai pelajaran yang menarik dan menyenangkan...
Pages - Menu
▼
Pages - Menu
▼
Saturday, 30 January 2016
Friday, 29 January 2016
Kuadran-Kuadran Trigonometri dan Nilainya
Jika kita lukis pada diagram cartesius, terdapat empat kuadran (wilayah) dalam trigonometri, seperti berikut:
Berdasarkan gambar diatas, diketahui bahwa :
Kuadran I bersudut 00 - 900
Jika
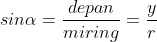
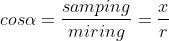
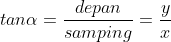
maka didapat bahwa,
Pada kuadran I,
nilai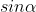 ,
,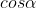 , dan
, dan 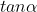 selalu positif karena sumbu x dan sumbu y selalu positif di kuadran I
selalu positif karena sumbu x dan sumbu y selalu positif di kuadran I
Pada kuadran II,
Nilai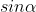 selalu positif, sedangkan nilai dari
selalu positif, sedangkan nilai dari 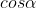 dan
dan 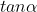 selalu negatif karena sumbu x bernilai negatif dan sumbu y bernilai positif di kuadran II.
selalu negatif karena sumbu x bernilai negatif dan sumbu y bernilai positif di kuadran II.
Pada kuadran III,
Nilai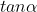 selalu positif, sedangkan nilai dari
selalu positif, sedangkan nilai dari 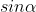 dan
dan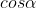 selalu negatif karena sumbu x bernilai negatif dan sumbu y bernilai negatif di kuadran III.
selalu negatif karena sumbu x bernilai negatif dan sumbu y bernilai negatif di kuadran III.
Pada kuadran IV,
Nilai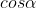 selalu positif, sedangkan nilai dari
selalu positif, sedangkan nilai dari 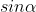 dan
dan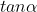 selalu negatif karena sumbu x bernilai positif dan sumbu y bernilai negatif di kuadran IV.
selalu negatif karena sumbu x bernilai positif dan sumbu y bernilai negatif di kuadran IV.
Sedangkan untuk menentukan nilai sinus, cosinus, dan tangen dari sudut-sudut tersebut, kita gunakan ketentuan berikut:
Kuadran II
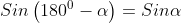
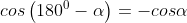
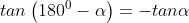
Kuadran III



Kuadran IV
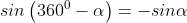
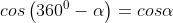
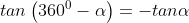
Contoh soal:
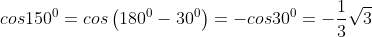

Berdasarkan gambar diatas, diketahui bahwa :
Kuadran I bersudut 00 - 900
Jika
maka didapat bahwa,
Pada kuadran I,
nilai
Pada kuadran II,
Nilai
Pada kuadran III,
Nilai
Pada kuadran IV,
Nilai
Sedangkan untuk menentukan nilai sinus, cosinus, dan tangen dari sudut-sudut tersebut, kita gunakan ketentuan berikut:
Kuadran II
Kuadran III
Kuadran IV
Contoh soal:
Thursday, 28 January 2016
Pembahasan Soal Olimpiade Pola Bilangan, barisan, dan Deret
Sebelumnya, postingan ini penulis tulis berdasarkan pertanyaan dari Siti Maimunah mengenai soal barisan dan deret. Semoga bermanfaat!
Wednesday, 27 January 2016
Cara Membuat Sketsa Fungsi Kuadrat
Fungsi kuadrat dinyatakan dalam  ,dengan
,dengan . Grafik dari fungsi kuadrat berbentuk kurva parabola. Berikut ini adalah langkah-langkah dalam melukis kurva tersebut!
. Grafik dari fungsi kuadrat berbentuk kurva parabola. Berikut ini adalah langkah-langkah dalam melukis kurva tersebut!
1. Tentukan titik potong sumbu x (x intercept) dengan y= 0!
2. Tentukan titik potong sumbu y (y intercept) dengan x= 0!
3. Tentukan persamaan sumbu simetri dengan menggunakan rumus !
!
4. Tentukan nilai maksimum/minimum dengan menggunakan rumus atau dapat juga dengan mensubstitusikan nilai yang didapat dari persamaan sumbu simetri kedalam fungsi!
atau dapat juga dengan mensubstitusikan nilai yang didapat dari persamaan sumbu simetri kedalam fungsi!
5. Tentukan koordinat titik balik berdasarkan nilai yang didapat dari langkah 3 dan 4!
6. Lukislah diagram cartesius dan hubungkan titik-titik yang diperoleh dari langkah 1 hingga langkah 5 menjadi sebuah kurva mulus!
7. Kurva parabola siap disajikan.
Contoh soal!
 ,dengan
,dengan . Grafik dari fungsi kuadrat berbentuk kurva parabola. Berikut ini adalah langkah-langkah dalam melukis kurva tersebut!
. Grafik dari fungsi kuadrat berbentuk kurva parabola. Berikut ini adalah langkah-langkah dalam melukis kurva tersebut!1. Tentukan titik potong sumbu x (x intercept) dengan y= 0!
2. Tentukan titik potong sumbu y (y intercept) dengan x= 0!
3. Tentukan persamaan sumbu simetri dengan menggunakan rumus
 !
!4. Tentukan nilai maksimum/minimum dengan menggunakan rumus
 atau dapat juga dengan mensubstitusikan nilai yang didapat dari persamaan sumbu simetri kedalam fungsi!
atau dapat juga dengan mensubstitusikan nilai yang didapat dari persamaan sumbu simetri kedalam fungsi!5. Tentukan koordinat titik balik berdasarkan nilai yang didapat dari langkah 3 dan 4!
6. Lukislah diagram cartesius dan hubungkan titik-titik yang diperoleh dari langkah 1 hingga langkah 5 menjadi sebuah kurva mulus!
7. Kurva parabola siap disajikan.
Contoh soal!
Monday, 25 January 2016
Soal Try Out UN SMP 2016
Assalamualaikum,
Pada postingan kali ini, penulis ingin berbagi mengenai soal latihan ujian nasional atau lebih umumnya disebut soal try out SMP, mengingat Ujian Nasional tinggal beberapa bulan lagi. Semoga bermanfaat!
Atau dapat juga mengunduh filenya disini
Atau dapat juga mengunduh filenya disini
Saturday, 23 January 2016
Pembelajaran Peluang Empirik di Sekolah
Salah satu bidang ilmu matematika dalam sekolah menengah yang paling menarik bagi saya adalah ilmu peluang. Peluang atau lebih populernya disebut probabilitas adalah kemungkinan suatu kejadian, suatu ukuran tentang kemungkinan atau derajat ketidakpastian suatu peristiwa (event) yang akan terjadi di masa mendatang. (dikuti dari http://sainsmatika.blogspot.co.id ). Derajat atau nilai maksimal dari peluang sebuah kejadian adalah 1 (satu) dan derajat atau nilai minimumnya adalah 0 (nol). Peluang yang bernilai nol diartikan suatu kejadian yang mustahil terjadi, sedangkan peluang yang bernilai 1 diartikan suatu kejadian yang pasti terjadi, dan peluang yang bernilai antara 0 dan 1 berarti kejadian yang mungkin dapat terjadi atau mungkin tidak terjadi. Perhatikan contoh ketiga kejadian di bawah ini! Malam itu Jadin dan Tono menonton pertandingan piala Eropa di televisi bersama dengan teman-temannya, Negara yang bertanding saat itu adalah Kroasi melawan Spanyol. Hingga akhir babak pertama, skor adalah 2-2. Berdasarkan ilustrasi tersebut, dapat dikatakan bahwa:
- Jadin dan Tono menonton pertandingan piala Eropa adalah kejadian yang pasti (benar benar terjadi) dan peluangnya adalah 1.
- Hasil akhir pertandingan merupakan kejadian yang belum terjadi, karena babak kedua belum terjadi, sehingga jika ditanya apakah tim Spanyol yang akan menang, maka jawabnya adalah bisa menang bisa juga kalah. (nilai peluang antara 0 dan 1).
- Jika ditanya apakah Jerman bermain pada pertandingan tersebut? maka peluang Jerman bermain pada pertandingan tersebut adalah 0 atau mustahil, karena kesebelasan yang bertandingan adalah kesebelasan Kroasia dan Spanyol.
Dalam pendekatan klasik, peluang sebuah kejadian diperoleh dari pembagian antara titik sampel (kejadian yang diharapkan untuk terjadi) dengan ruang sampel (seluruh kejadian yang dapat terjadi. Dengan kata lain,
Contoh:
Jika Amir melempar sebuah koin dan dia menghendaki keluar adalah sisi koin yang bertuliskan angka, maka banyak titik sampel dari pelempar koin adalah 1 dan banyak ruang sampel dari koin tersebut adalah 2 (koin memiliki 2 sisi). Sehingga peluang dari pelemparan tersebut adalah
Sedangkan dalam peluang empirik, nilai peluang ditentukan melalui kegiatan eksperiment terhadap sebuah objek. Sebagai contoh:
Untuk menentukan peluang keluarnya sisi angka dari sebuah koin logam, kita lakukan dengan percobaaan melempar koin tersebut secara berulang ulang. hasil yang diperoleh tiap lemparan kita catat. Setelah selesai melempar, kita jumlah banyak angka yang keluar dari semua pelemparan yang sudah dilakukan. Kemudian kita tentukan nilai peluang dengan membagi antara banyak angka yang keluar dengan banyak kejadian dalam pelemparan.Berdasarkan hasil percobaan itulah kita kemudian tarik kesimpulan bahwa peluang nilai yang didapat mengarah
Hingga kini, pendekatan pembelajaran yang digunakan di tingkat sekolah menengah kebanyakan menggunakan pendekatan klasik, yakni nilai dari peluang ditentukan oleh hasil bagi antara banyak titik sampel dan banyak ruang sampel. Hal itu dikarenakan pada pembelajaran peluang ini seorang pengajar tidak memerlukan alat peraga dan tidak memakan banyak waktu. Selain itu, pembelajaran peluang empirik masih sangat asing.
Meskipun demikian, bukan berarti pendekatan empirik tidak perlu dilakukan. Pendekatan empirik sangat penting bagi siswa. Melalui pendekatan empirik, siswa belajar peluang secara konkret. Siswa dapat melakukan pengamatan terhadap alat peraga yang diberikan oleh guru yang kemudian dia tuliskan hasil pengamatan tersebut dalam laporan mereka. Setelah mereka melakukan pengamatan dan penulisan data, siswa dapat menyimpulkan hasil pengamatan dan membandingkan dengan peluang kejadian yang lain. Melalui kegiatan tersebut manfaat yang didapatkan oleh siswa yakni siswa belajar melakukan kegiatan saintifik sederhana. Selain itu, melalui kegiatan ini akan memunculkan gagasan-gagasan baru pada diri siswa terkait masalah peluang.
Selain itu, manfaat lain yang diperoleh siswa melalui pembelajaran peluang empirik adalah , siswa dapat menghubungkan pembelajaran matematika dan pembelajaran karakter, Misalnya jika didalam pembelajaran peluang klasik, peluang keluarnya gambar dari pelemparan sebuah koin adalah setengah, artinya apapun situasi dan suasananya peluangnya pasti setengah. Namun tidak demikian untuk peluang empirik. Jika kita melakukan percobaan melempar sebuah koin sebanyak n kali (misalnya 500 kali). Bisa saja lemparan pertama hingga lemparan ke-499 selalu muncul angka dan ketika lemparan ke-500 barulah muncul gambar. Arti dari contoh tersebut adalah melukiskan seorang siswa yang dianggap kurang pandai dan sering mendapatkan nilai yang kurang baik dalam ujian (diibaratkan dengan sisi angka yang muncul hingga 499). Namun berkat ketekunan dan keseriusannya dalam mengerjakan ujian, pada ujian akhir nasional dia berhasil mendapatkan nilai yang terbaik (seperti halnya sisi gambar yang muncul pada pelemparan ke-500). Jika siswa kita memahami demikian, tentu akan menjadi motivasi tersendiri bagi diri mereka. Sedangkan jika kita berpedoman pada peluang klasik, seorang siswa yang selalu mendapatkan jelek dalam ujian, dia akan terus merasa mendapatkan nilai ujian yang jelek untuk ujian berikutnya karena merasa peluangnya sangat kecil sekali untuk dia mendapatkan nilai ujian yang bagus.
Semoga artikel yang sederhana ini bisa bermanfaat buat teman-teman semua. Kritik dan sarannya sangat ditunggu. Salam!
Sunday, 10 January 2016
Soal UAS Matematika Semester Ganjil Kelas 9
Assalamualaikum,
Sudah lama sekali nih, penulis tidak memposting seusuatu kedalam blog ini. Untuk memulainya, pada kesempatan kali ini penulis ingin berbagi mengenai soal latihan Ulangan Akhir semester matematika kelas 9 dengan harapan dapat digunakan sebagai tambahan referensi belajar matematika. Semoga bermanfaat!
Thursday, 7 January 2016
Ar Rohmah Festival 2016 (AFEST)
Assalamualaikum, Pada postingan kali ini, penulis ingin berbagi mengenai info lomba Ar Rohmah Fastival. Ar Rohmah festivas adalah salah satu event tahunan yang diadakan oleh SMP Ar Rohmah. Bidang-bidang yang dilombakan dalam Ar Rohmah Festival antara lain:
Lomba Tahfidzul Quran
Lomba Tilawatul Quran
Story Telling
Olimpiade Matematika
OlimpiadeSains
Oh iya, keseluruhan lomba ini adalah lomba tingkat sekolah dasar (SD). Penasaran, ini adalah brosur dari AFEST 2016
Lomba Tahfidzul Quran
Lomba Tilawatul Quran
Story Telling
Olimpiade Matematika
OlimpiadeSains
Oh iya, keseluruhan lomba ini adalah lomba tingkat sekolah dasar (SD). Penasaran, ini adalah brosur dari AFEST 2016







