Olimpiade KMNR adalah salah satu olimpiade matematika yang diadakan oleh Klinik Pendidikan MIPA untuk mengasah kompetensi siswa. Pada tahun ini juga diadakan olimpiade KMNR yang diadakan untuk para guru matematika. Sebagai bahan belajar, pada postingan kali ini penulis ingin berbagi mengenai soal dan pembahasan olimpiade KMNR guru, namun sebatas nomor 1-16, sedangkan untuk nomor yang lain dalam proses pengetikan. Semoga bermanfaat!
Untuk file dapat diunduh disini
Mari kita jadikan matematika sebagai pelajaran yang menarik dan menyenangkan...
Pages - Menu
▼
Pages - Menu
▼
Wednesday, 20 April 2016
Tuesday, 19 April 2016
Cara Memanipulasi Aljabar
Aljabar adalah salah satu bidang dalam pelajaran matematika yang dapat dibilang agak unik. Mengapa demikian? Hal ini dikarenakan pada aljabar, kita diminta memiliki kemampuan untuk memanipulasi variabel dan bilangan untuk memperoleh suatu penyelesaian. Namun, bagi kebanyakan siswa, kemampuan memanipulasi ini agak susah. Selain harus terbiasa, mereka harus menggunakan kemampuan menghubungkan antara konsep satu dengan konsep yang lain serta kemampuan bernalar dan mengalanalisa. Pada kesempatan kali ini penulis ingin berbagi soal latihan dan penyelesaian mengenai bagaimana cara memanipulasi bentuk aljabar. Semoga bermanfaat!
Monday, 4 April 2016
4 Cara Menentukan Luas Segitiga
1. Rumus luas segitiga yang umum
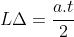
Berdasarkan gambar diatas, diketahui bahwa segitiga ABC diketahui panjang sisi-sisinya adalah
a, b, dan c. Luas segitiga dapat ditentukan dengan rumus:
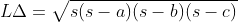 dengan
dengan 
Berdasarkan gambar diatas, diketahui Panjang sisi AB= c cm, sisi BC= a cm, dan sudut antara AB dan BC adalah x0. Luas segitga dapat ditentukan dengan menggunakan rumus:

4. Rumus Segitga Pada Koordinat Cartesius
Rumus ini sangat efektif sekali ketika kita menentukan luas dari segitiga pada koordinat cartesius jika diketahui titik-titik sudut pada segitiga tersebut. Pendekatan yang digunakan dalam
menentukan luas adalah menggunakan pendekatan determinan matriks.
Misalkan A(a,b), B(c,d) dan C(e,f) membentuk segitiga
Mungkin pembaca bingung mengapa saya sebut
sebagai rumus luas segitiga yang umum, hal ini dikarenakan rumus segitiga ini
sangat sering digunakan dalam perhitungan bangun datar atau
bangun ruang.
Selain itu, rumus ini sudah diperkenalkan kepada siswa mulai mereka duduk di
bangku Sekolah Dasar. Langsung saja, perhatikan gambar di bawah ini!
Jika t menyatakan tinggi segitiga dan a menyatakan
alas segitiga, maka luas segitiga adalah
Rumus ini sangat efektif digunakan ketika alas dan
tinggi segitiga diketahui.
2. Rumus Heron
Rumus luas segitiga yang kedua adalah rumus
heron. Rumus ini diturunkan dari aturan kosinus
dan prinsip segitiga. Kelebihan
dari rumus ini adalah kita tidak perlu menentukan tinggi segitiga terlebih
dahulu untuk menentukan luas dari segitiga, namun cukup diketahui ukuran
panjang dari sisi-sisi segitiga. Perhatikan gambar di bawah ini!
Berdasarkan gambar diatas, diketahui bahwa segitiga ABC diketahui panjang sisi-sisinya adalah
a, b, dan c. Luas segitiga dapat ditentukan dengan rumus:
Rumus ini sangat efektif digunakan ketika semua
panjang sisi segitiga diketahui ukurannya.
3. Rumus segitiga dengan menggunakan sinus (Sin)
Jika suatu segitiga dua buah sisinya diketahui ukurannya dan sebuah sudut apit antara kedua sisi tersebut diketahui pula, Maka dapat kita tentukan luas segitiga dengan menggunakan pendekatan
sinus, seperti berikut:
Berdasarkan gambar diatas, diketahui Panjang sisi AB= c cm, sisi BC= a cm, dan sudut antara AB dan BC adalah x0. Luas segitga dapat ditentukan dengan menggunakan rumus:
4. Rumus Segitga Pada Koordinat Cartesius
Rumus ini sangat efektif sekali ketika kita menentukan luas dari segitiga pada koordinat cartesius jika diketahui titik-titik sudut pada segitiga tersebut. Pendekatan yang digunakan dalam
menentukan luas adalah menggunakan pendekatan determinan matriks.
Misalkan A(a,b), B(c,d) dan C(e,f) membentuk segitiga
maka luas
segitiga dapat ditentukan dengan rumus:
Selain digunakan
untuk menentukan luas segitiga, cara ini dapat dikembangkan untuk
menentukan
luas segi-n pada koordinat kartesius.
Demikian keempat
cara menentukan luas segitiga. Semoga artikel ini bermanfaat bagi pembaca
sekalian.







