Soal Persiapan Ulangan Akhir Semester Ganjil Matematika Kelas 9

Tidak terasa, seminggu lagi ulangan akhir semester ganjil tiba. Untuk mendapatkan hasil yang maksimal, banyak persiapan yang perlu dilakukan, terutama pada mata pelajaran matematika yang selama ini dianggap sebagai pelajaran "susah". Untuk membantu belajar adik-adik semua, pada postingan kali ini penulis ingin berbagi soal latihan matematika kelas 9 sebagai bahan belajar mempersiapkan ulangan akhir semester ganjil. Semoga bermanfaat!

Atau dapat download filenya disini

Pembahasan KMNR 2015 Babak Penyisihan nomor 22 dan 23

Assalamualaikum sobat semua,Pada postingan kali ini penulis ingin berbagi mengenai pembahasan soal babak penyisihan KMNR 11 yang dilaksanakan pada tanggal 29 November 2015 kemarin. Namun karena kesibukan penulis, penulis mencoba mengulasnya sedikit demi sedikit. Semoga bermanfaat!

Soal No. 22
Dimisalkan k adalah bilangan bulat. Jika persamaan kuadrat 6x²-3(k-1)x+k²-97=0 memiliki dua akar bilangan negative yang berbeda, maka nilai k adalah ....

Penyelesaian:
Jika suatu persamaan kuadrat memiliki akar-akar bilangan negatif yang berbeda, maka:

x₁+x₂ < 0 ......................... (1)

x₁.x₂ > 0 .......................... (2)

Untuk syarat pertama

x₁+x₂ < 0 .








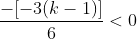
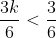
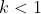
Untuk syarat kedua
x_1.x_{2 >} 0





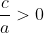
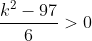
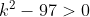
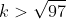 atau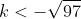 

Daerah yang memenuhi kedua interval tersebut adalah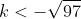 
Berdasarkan opsi jawaban, jawaban d dan e sudah tidak mungkin karena d dan e positif. Untuk selanjutnya kita dapat melakukan substitusi -1, -13, dan -14 kedalam k agar ditemukan jawaban yang tepat, Misal kita coba x= -3, maka




x = -4 atau x = -3 (Bilangan bulat negetif berbeda)
Jawaban B

Soal No. 23
Diketahui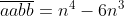  untuk n bilangan bulat, dimana  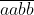merupakan bilangan 4 angka yang nilai a dan b bilangan bulat tidak nol. Tentukan hasil kali dari a dan b!

Penyelesaian:
aabb= 1000a+100a+10b+b
aabb= 1100a+11b
aabb= 11(100a+b)
Sehingga kita ketahui bahwa aabb adalah bilangan kelipatan 11.


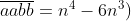
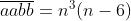
Misalkan n=11, maka



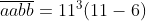
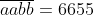
dapat diketahui bahwa a= 6 dan b= 5
axb= 6x5
axb= 30
Jawaban E



 .

Rata-rata Kuadrat, Aritmatik, Geometri, dan Harmonik (AM-GM)

Sebenarnya tulisan ini berasal dari Bapak Syaiful Arif, namun karena beliaunya menyetujui  maka saya ingin berbagi dengan teman-teman sekalian, semoga bermanfaat!


Atau download di disini

Ide Mudah Mengisi Persegi Ajaib Bagian 2

Pada postingan sebelumnya, penulis telah menjelaskan mengenai bagaimana trik mengisi kotak-kotak pada persegi ajaib (Ide Mudah Mengisi Persegi Ajaib). Pada kesempatan kali ini, kita akan menyelidiki apakah perasegi ajaib dapat diisi dengan sembarang bilangan bulat dengan beda tiap langkah adalah sama.

Misalkan baris kedua kolom pertama kita isi dengan a (dengan a adalah bilangan bulat), maka

Jika selisih bilangan tiap langkah adalah b, maka persegi ajaib tersebut menjadi

Sekarang kita coba cek.

Jumlah bilangan baris pertama: a+7b+a+a+5b       = 3a+12b

Jumlah bilangan baris kedua   : a+2b+a+4b+a+6b = 3a+12b

Jumlah bilangan baris ketiga   : a+3b+a+8b+a+b   = 3a+12b

Jumlah bilangan kolom pertama: a+7b+a+2b+a+3b= 3a+12b

Jumlah bilangan kolom kedua   : a+a+4b+a+8b       = 3a+12b

Jumlah bilangan kolom ketiga   : a+5b+a+6b+a+b   = 3a+12b

Jumlah diagonal pertama            : a+7b+a+4b+a+b   = 3a+12b

Jumlah diagonal kedua               : a+5b+a+4b+a+3b = 3a+12b               

Ide Mudah Mengisi Persegi Ajaib

Pada postingan kali ini, penulis ingin berbagi mengenai bagaimana cara mengisi persegi ajaib (magic square) dengan cepat dan akurat. Persegi ajaib adalah sebuah persegi yang didalam terbagi-bagi lagi menjadi n x n persegi. Pada pada tiap bagian dalam persegi kecil tersebut harus diisi dengan sebuah bilangan sehingga jumlah bilangan pada sisi horizontal, vertikal, dan diagonal pada persegi besar (keseluruhan) adalah sama. Sebagai contoh adalah persegi ajaib berikut:

Persegi ajaib diatas merupakan persegi ajaib berukuran 3x3. Pada persegi besar, jumlah bilangan pada sisi horizontal selalu sama dengan jumlah bilangan pada sisi vertikal dan selalu sama pula dengan jumlah bilangan pada diagonal, yakni 15.

Dalam pembelajaran, persegi ajaib ini dapat digunakan sebagai salah satu variasi pembelajaran, terutama pembelajaran yang berhubungan dengan bilangan. Karena secara tidak langsung mereka belajar mengenai pola bilangan dan operasi bilangan. Selain itu persegi ajaib juga digunakan sebagai  penyegaran otak (rekreatif) ketika siswa sudah penat belajar matematika.

Yang menjadi pertanyaan, jika persegi ajaib adalah sebuah pola bilangan apakah ada rahasia dalam mengisi tiap kotaknya? Tentu saja ada, karena jika jumlah tiap baris, kolom, dan diagonal selalu ditentukan sama pasti ada pola didalamnya. Perhatikan gambar di bawah ini!

Pada gambar diatas, diketahui sebuah persegi ajaib berukuran 5x5 dengan hanya diketahui bilangan pada baris pertama kolom ketiga, yakni 2. Sekarang kita akan melengkapi semua kotak yang masih kosong. Ketentuan dari pengisian kotak sebagai berikut:

Isilah kotak dengan bilangan setelah bilangan yang sudah diketahui (dalam contoh ini 2) dengan arah diagonal kekanan atas secara berturut-turut. Jika kotak yang dimaksud sudah tidak tersedia, maka isi  kotak paling bawah (baris 5 kolom 4). 

Kemudian, isi kotak selanjutnya secara diagonal dengan arah kanan atas. 

Karena tidak ada kotak dengan arah diagonal keatas setelah 4, maka isi pada kotak paling kiri (baris 3  kolom 1)

Karena atas dari kotak bernomor 6 telah terisi (nomor 2), maka kotak di bawah kotak nomor 6 yang harus diisi (baris 3 kolom 2).

Dengan menggunakan ketentuan diatas, isilah kotak-kotak tersebut dengan bilangan berurutan hingga kotak penuh. Untuk memastikan apakah telah memenuhi ketentuan dari persegi ajaib, cobalah cek jumlah perbaris, kolom, dan diagonal.

Langkah ini juga berlaku kedalam persegi ajaib berukuran n x n dengan n adalah bilangan ganjil dan selisih bilangan tiap langkah adalah sama. Baca kelanjutannya di Ide Mudah Mengisi Persegi Ajaib Bagian 2 .

Hubungan Antara Kerucut dan Bola

Pada postingan kali ini, penulis ingin berbagi mengenai hubungan antara kerucut dan bola. Jika sebuah bola dimasukkan kedalam kerucut sedemikian hingga ujung-ujung dari bola menempel pada sebuah kerucut, maka kita dapat menentukan jari-jari, tinggi, garis selimut, volume, dan luas permukaan kerucut jika diketahui jari-jari bola tersebut. Perhatikan gambar di bawah ini!

  

Sekian dulu penjelasan dari penulis mengenai kerucut dan bola. Mohon maaf atas tampilannya yang kurang rapi, mengingat dalam penulisannya agak terburu-buru. Penulis tunggu kritik dan sarannya.

Tips Mudah Menentukan Volume dari Kerucut Terpancung

 Pada postingan kali ini, penulis ingin berbagi mengenai bagaimana cara menentukan volume dari sebuah kerucut terpancung. Ide awal dari tulisan ini adalah secara tidak sengaja ketika penulis memberikan les privat kepada seorang siswa SMP mengenai bangun ruang sisi lengkung. Pada pembahasan mengenai kerucut terpancung, dia merasa tidak puas dan berusaha mencari bagaimana cara menentukan rumus volume dari sebuah kerucut terpancung. Alhasil, kita (penulis dan siswa) mendapatkan cara sederhana tersebut, kalau begitu langsung saja kita ulas.

Perhatikan gambar di bawah ini!

Volume dari bangun diatas adalah ....

Penyelesaian:

Untuk menyelesaikan permasalahan diatas, kita perlu memberikan memberikan garis bantu yang menandakan bangun tersebut adalah potongan dari kerucut.

Berdasarkan hasil diatas, maka untuk menentukan tinggi CD dan CO dapat kita gunakan teorema phytagoras, diperoleh CD= 3 cm dan CO= 9 cm.

Langkah berikutnya adalah menentukan volume dari kerucut terpancung, yakni

Konsep ini dapat kita kembangkan untuk kerucut terpancung dengan perbandingan jari-jari m dan n. Perhatikan contoh di bawah ini!

Demikian tips dari penulis, kritik dan saran senantiasa diharapkan, mengingat masih banyaknya kekurangan akan tulisan penulis. 

Berdasarkan soal diatas, maka 

DB= 4= 4x1

OA= 12= 4x3

CD= 3 cm= 3x1

CO= 9 cm= 3x3

Beberapa Fakta Unik tentang Segitiga Pascal

Bagi matholic, mungkin istilah segitiga pascal bukan sesuatu hal yang asing lagi. Segitiga pascal adalah suatu aturan geometri pada koefisien binomial dalam sebuah segitiga (https://id.wikipedia.org/wiki/Segitiga_Pascal). Segitiga pascal diperkenalkan kali oleh Blaise pascal, meskipun beradad-abad sebelumnya sudah banyak dikaji oleh ilmuwan-ilmuwan India, Persia, Cina, dan Italia. Berikut ini adalah beberapa fakta unik seputar segitiga pascal.

Jumlah bilangan dari tiap barisnya adalah 2⁰, 2¹, 2², 2³, ... 
Perhatikan pola bilangan segitiga berikut ini!

Jika kita perhatikan, jumlah bilangan pada baris pertama adalah 1= .
Jumlah bilangan pada baris kedua adalah 1+1= 2= 2¹.
Jumlah bilangan pada baris ketiga adalah 1+2+1= 4= 2².
Jumlah bilangan pada baris ketiga adalah 1+3+3+1= 8= 2³.
dst.
Jumlah bilangan pada baris ke-n adalah 1+ ...+1= 2^n-1

Segitiga pascal digunakan untuk menentukan probabilitas pelemparan n buah koin.
Selain aplikasi dalam bentuk bilangan, segitiga pascal juga dapat diaplikasikan dalam ilmu probabilitas atau peluang, yakni untuk menentukan ruang sampel, titik sampel, dan peluang dari pelemparan n buah koin.
Perhatikan gambar segitiga pascal diatas!
Jumlah bilangan pada baris kedua adalah 1+1= 2, yakni sama dengan jumlah ruang sampel pada pelemparan sebuah koin. 1 merupakan titik sampel dari sebuah angka dan 1 merupakan titik sampel dari sebuah gambar.
Jumlah bilangan pada baris ketiga adalah 1+2+1= 4, yakni sama dengan jumlah ruang sampel pada pelemparan dua buah koin. 1 merupakan titik sampel dari 2 buah angka, 2 adalah titik sampel dari sebuah angka dan sebuah gambar, dan 1 adalah titik sampel dari dua buah gambar.
Jumlah bilangan pada baris keempat adalah 1+3+3+1= 8, yakni sama dengan jumlah ruang sampel pada pelemparan tiga buah koin. 1 merupakan titik sampel dari 3 buah angka, 3 adalah titik sampel dari dua angka dan sebuah gambar, 3 adalah titik sampel dari sebuah angka dan dua buah gambar dan 1 adalah titik sampel dari 3 buah gambar.
Jumlah bilangan pada baris kelima adalah 1+4+6+4+1= 16, yakni sama dengan jumlah ruang sampel pada pelemparan empat buah koin. 1 merupakan titik sampel dari 4 buah angka, 4 adalah titik sampel dari tiga angka dan sebuah gambar, 6 adalah titik sampel dari dua angka dan dua buah gambar, 4adalah titik sampel dari sebuah angka dan tiga buah gambar dan 1 adalah titik sampel dari 4 buah gambar.
Ketentuan ini perlaku seterusnya hingga n buah koin.

Segitiga pascal digunakan untuk menentukan banyak himpunan bagian 
Dalam ilmu himpunan, segitiga pascal juga digunakan untuk menentukan banyaknya himpunan bagian dari sebuah himpunan.
Jumlah bilangan pada baris kedua adalah 1+1= 2, yakni sama dengan banyak himpunan bagian pada himpunan yang beranggotakan satu anggota. 1 adalah  banyak himpunan kosong dan 1 adalah banyak himpunan bagian yang beranggotakan satu anggota.
Jumlah bilangan pada baris ketiga adalah 1+2+1= 4, yakni sama dengan banyak himpunan bagian pada himpunan yang beranggotakan dua anggota. 1 adalah banyak himpunan kosong, 2 adalah banyak himpunan bagian yang beranggotakan satu anggota, dan 1 adalah banyak himpunan bagian yang beranggotakan dua anggota.
Jumlah bilangan pada baris keempat adalah 1+3+3+1= 8, yakni sama dengan banyak himpunan bagian pada himpunan yang beranggotakan tiga anggota. 1 adalah banyak himpunan kosong, 3 adalah banyak himpunan bagian yang beranggotakan satu anggota, 3 adalah banyak himpunan bagian yang beranggotakan dua anggota, dan 1 adalah banyak himpunan bagian yang beranggotakan tiga anggota.
Jumlah bilangan pada baris kelima adalah 1+4+6+4+1= 16, yakni sama dengan banyak himpunan bagian pada himpunan yang beranggotakan empat anggota. 1 adalah banyak himpunan kosong, 4 adalah banyak himpunan bagian yang beranggotakan satu anggota, 6 adalah banyak himpunan bagian yang beranggotakan dua anggota, 4 adalah banyak himpunan bagian yang beranggotakan tiga anggota, dan 1 adalah banyak himpunan bagian yang beranggotakan empat anggota.

Segitiga pascal digunakan untuk menentukan lintasan terpendek.
Hal menarik terakhir dari segitiga pascal yakni konsep segitiga pascal dapat diaplikasikan dalam kehidupan sehari-hari, yakni untuk menentukan lintasan terpendek dari sebuah jalan. Contoh:
Perhatikan gambar di bawah ini!

Seorang wisatawan ingin mengunjungi taman bermain terbaru di sebuah kota. Ketika sampai di depan gerbang, dia harus melewati perumahan untuk sampai ke taman bermain tersebut. Banyak lintasan terpendek yang dapat dilalui wisatawan adalah ....
Penyelesaian:
Untuk menentukan banyak lintasan terpendek agar sampai ke taman bermain, kita gunakan konsep segitiga pascal sebagai berikut:

Berdasarkan perhitungan diatas, maka banyak lintasan terpendek yang dapat dilalui adalah 10 lintasan.
Itulah beberapa fakta unik seputar segitiga pascal. Semoga bermanfaat!

Pembahasan Soal Final Fachrudin Ar Razi Competition Tahun 2013

Fachrudin Ar Razi merupakan salah satu event tahunan yang diselenggarakan oleh KPM bekerjasama dengan majalah gontor. Berbeda dengan kompetisi-kompetisi lainnya, Kompetensi yang diujikan didalam Fachrudin Ar Razi Competition adalah Studi agama islam dan matematika. Sebagai bahan belajar, pada postingan kali ini penulis ingin berbagi soal final Fachrudin Ar Razi tahun 2013beserta pembahasannya, mohon koreksinya dan semoga bermanfaat! Download file disini