Soal No. 22
Dimisalkan k adalah bilangan bulat. Jika persamaan kuadrat 6x2-3(k-1)x+k2-97=0 memiliki dua akar bilangan negative yang berbeda, maka nilai k adalah ....
Penyelesaian:
Jika suatu persamaan kuadrat memiliki akar-akar bilangan negatif yang berbeda, maka:
x1+x2 < 0 ......................... (1)
x1.x2 > 0 .......................... (2)
Untuk syarat pertama
x1+x2 < 0 .

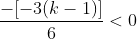


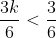
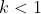
Untuk syarat kedua
x1.x2 > 0
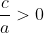
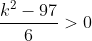

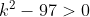

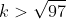 atau
atau 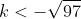
Daerah yang memenuhi kedua interval tersebut adalah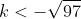
Berdasarkan opsi jawaban, jawaban d dan e sudah tidak mungkin karena d dan e positif. Untuk selanjutnya kita dapat melakukan substitusi -1, -13, dan -14 kedalam k agar ditemukan jawaban yang tepat, Misal kita coba x= -3, maka




x = -4 atau x = -3 (Bilangan bulat negetif berbeda)
Jawaban B
Soal No. 23
Diketahui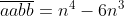 untuk n bilangan bulat, dimana
untuk n bilangan bulat, dimana 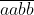 merupakan bilangan 4 angka yang nilai a dan b bilangan bulat tidak nol. Tentukan hasil kali dari a dan b!
merupakan bilangan 4 angka yang nilai a dan b bilangan bulat tidak nol. Tentukan hasil kali dari a dan b!
Penyelesaian:
aabb= 1000a+100a+10b+b
aabb= 1100a+11b
aabb= 11(100a+b)
Sehingga kita ketahui bahwa aabb adalah bilangan kelipatan 11.
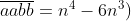
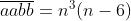
Misalkan n=11, maka
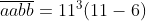

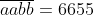
dapat diketahui bahwa a= 6 dan b= 5
axb= 6x5
axb= 30
Jawaban E
.
Untuk syarat kedua
x1.x2 > 0
Daerah yang memenuhi kedua interval tersebut adalah
Berdasarkan opsi jawaban, jawaban d dan e sudah tidak mungkin karena d dan e positif. Untuk selanjutnya kita dapat melakukan substitusi -1, -13, dan -14 kedalam k agar ditemukan jawaban yang tepat, Misal kita coba x= -3, maka
x = -4 atau x = -3 (Bilangan bulat negetif berbeda)
Jawaban B
Soal No. 23
Diketahui
Penyelesaian:
aabb= 1000a+100a+10b+b
aabb= 1100a+11b
aabb= 11(100a+b)
Sehingga kita ketahui bahwa aabb adalah bilangan kelipatan 11.
Misalkan n=11, maka
dapat diketahui bahwa a= 6 dan b= 5
axb= 6x5
axb= 30
Jawaban E
.
No comments:
Post a Comment