Pembahasan Latihan Soal Matematika 4

Question:
Consider the following figure!

The height of tower from above figure is ....

Answer:
First, determine the distance between the sea level with the base tower. Use phytagorean theorem!

Because of the angle, 45 degrees, 45 degrees, and 90 degrees, then the triangle is right-angled isosceles. If the base and height of the triangle we let x, then:
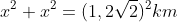
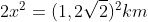
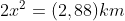
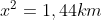
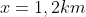
This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

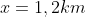
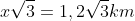
This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

Next, determine the distance between the sea level with the top tower

According the ratio comparison of special angles in a triangle, known comparison side front corner of 30 degrees, 60 degrees, and 90 degrees are This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

, so:

The height of tower is the difference of distance between the sea level with the base tower and the distance between the sea level with the top tower, so that:
height of tower is This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

km.

Pembahasan Latihan Soal Matematika 4

Next

Newer Post

Previous

Older Post

0 comments: